一些不太好记的概念和公式

本章字数: 4k阅读时长: 13 分钟最后更新于: 26天前

✨

收集和计算题有关的一些概念和公式

挣值分析

EV、AC、PV、ETC、EAC、VAC等概念

EV（Earned Value）：即挣值，也被称作已完成工作预算成本
AC（Actual Cost）：是实际成本，即实际完成工作所花费的成本
PV（Planned Value）：代表计划价值，又称计划工作预算成本
BAC（Budget At Completion）：项目完工预算，指完成项目所有工作的总预算
CV（Cost Variance）：成本偏差，通过公式 CV = EV - AC 计算。当 CV > 0 ，表示 EV 大于 AC，成本节约
SV（Schedule Variance）：进度偏差，根据公式 SV = EV - PV 计算。SV > 0 时，EV 大于 PV，项目进度提前
SPI（Schedule Performance Index）：进度绩效指数，是项目管理中用于衡量项目进度效率的关键指标。SPI<1：实际工作量小于计划工作量（滞后），大于1（进度超前） SPI = EV / PV 例：SPI为80.00%时表示进度为正常进度的80%（滞后）
CPI（Cost Performance Index）：成本绩效指数，是项目管理中用于衡量成本效率的关键指标。CPI＞1：挣值大于实际成本，即实际成本低于预算，成本控制良好（有结余），CPI<1：实际成本超预算。 CPI = EV / AC 例：CPI为1.05时项目100元的成本创造了105元的价值
ETC：完工尚需估算，完成剩余工作还需要的成本估算
EAC：完工估算，完成整个项目预计需要的总成本

计算公式

CV = EV - AC >0 节省
SV = EV - PV >0 提前
CPI = EV / AC >1 节省
SPI = EV / PC >1 提前
典型：出现偏差后，还照原计划
- ETC = (BAC - EV) / CPI
- EAC = AC + ETC = AC + (BAC - EV) / CPI
非典型：出现偏差后，纠错/改善
- ETC = BAC - EV
- EAC = AC + ETC = AC + BAC - EV

⚡️非典型偏差记忆协助

因为前期出现了偏差然后又改善了，前面的偏差属于偶然原因或事件，所以称为非典型。计算ETC的时候不用除以CPI。

⚡️进度和成本偏差记忆协助

计划花费10元，10天买10个苹果。

9天的时候买了8个苹果，花费了7元。 EV = 8；PV = 9；AC = 7；

由此可直接推测：成本节省，进度滞后。

CPI = EV / AC = 8 / 7 > 1 成本节省； SPI = EV / PV = 8 / 9 < 1 进度滞后。

⚡️进度成本偏差时可采取措施

进度滞后，成本节约时可采取的措施（赶快两高两减）

赶工，投入更多的资源或增加工作时间，以缩短关键活动的工期（成本会增加）
快速跟进，并行施工，以缩短关键路径的长度
使用高素质的资源或经验更丰富的人员
减少活动范围或降低活动要求（甲方同意的前提）
改进方法或技术，以提高生产效率
加强质量管理，及时发现问题，减少返工，从而缩短工期

进度滞后，成本超支时：上面六条去除第一个赶工

进度超前、成本超支：

抽出部分人员
适当降低工作效率
适当安排休假

AI生成的帮助理解图表

✨点击展开

<!-- ✅ deepseek-r1 -->
──────────────────────────────────────
[基础数据]
  │
  ├─ PV（计划价值）：计划完成工作的预算价值
  ├─ EV（挣值）：实际完成工作的预算价值
  ├─ AC（实际成本）：实际发生的成本
  │
  ╰─▶ [绩效指标] 
       │
       ├─ 进度分析
       │   ├─ SV（进度偏差）= EV - PV
       │   │   ├─ >0：进度超前
       │   │   ╰─ <0：进度落后
       │   ╰─ SPI（进度绩效指数）= EV/PV
       │       ├─ >1：进度超前
       │       ╰─ <1：进度落后
       │
       ╰─ 成本分析
           ├─ CV（成本偏差）= EV - AC
           │   ├─ >0：成本节省
           │   ╰─ <0：成本超支
           ╰─ CPI（成本绩效指数）= EV/AC
               ├─ >1：成本节省
               ╰─ <1：成本超支

[预测指标]
  │
  ├─ BAC（完工预算）：项目总预算
  │
  ├─ ETC（完工尚需估算）= 
  │   ├─ (BAC - EV)/CPI → 典型绩效延续
  │   ╰─ 重新估算 → 特殊场景
  │
  ├─ EAC（完工估算）= AC + ETC
  │   ╰─ 或 = BAC/CPI → 典型公式
  │
  ╰─ VAC（完工偏差）= BAC - EAC
      ├─ >0：预计结余
      ╰─ <0：预计超支

<!-- ✅ qwen2.5-max 生成 -->
──────────────────────────────────────
+-----------------------------+
|          项目状态           |
|                             |
|   +----------------------+  |
|   |      实际成本 (AC)    |  |
|   | 已花费的实际金额 ($) |  |
|   +----------------------+  |
|                             |
|   +----------------------+  |
|   | 计划价值 (PV)         |  |
|   | 按计划应完成的预算 ($) |  |
|   +----------------------+  |
|                             |
|   +----------------------+  |
|   | 挪用价值 (EV)         |  |
|   | 实际完成工作的预算 ($) |  |
|   +----------------------+  |
+-----------------------------+

          ↓ 计算指标
+-----------------------------+
|       绩效指标             |
|                             |
|   +----------------------+  |
|   | 进度绩效指数 (SPI)    |  |
|   | SPI = EV / PV         |  |
|   | >1: 超前, <1: 落后    |  |
|   +----------------------+  |
|                             |
|   +----------------------+  |
|   | 成本绩效指数 (CPI)    |  |
|   | CPI = EV / AC         |  |
|   | >1: 节省, <1: 超支    |  |
|   +----------------------+  |
|                             |
|   +----------------------+  |
|   | 进度偏差 (SV)         |  |
|   | SV = EV - PV          |  |
|   | >0: 超前, <0: 落后    |  |
|   +----------------------+  |
|                             |
|   +----------------------+  |
|   | 成本偏差 (CV)         |  |
|   | CV = EV - AC          |  |
|   | >0: 节省, <0: 超支    |  |
|   +----------------------+  |
+-----------------------------+

          ↓ 预测未来
+-----------------------------+
|       预测指标             |
|                             |
|   +----------------------+  |
|   | 完工尚需估算 (ETC)    |  |
|   | ETC = (BAC - EV) / CPI | |
|   | 或重新估算剩余工作    |  |
|   +----------------------+  |
|                             |
|   +----------------------+  |
|   | 完工估算 (EAC)        |  |
|   | EAC = AC + ETC        |  |
|   | 或其他公式变体        |  |
|   +----------------------+  |
|                             |
|   +----------------------+  |
|   | 完工偏差 (VAC)        |  |
|   | VAC = BAC - EAC       |  |
|   | >0: 节省, <0: 超支    |  |
|   +----------------------+  |
+-----------------------------+

总时差、自由时差

总时差：指一项工作在不影响总工期的前提下所具有的机动时间
- 总时差 = LS - ES = LF - EF
指一项工作在不影响后续工作的情况下所拥有的机动时间
- 自由时差 = min(紧后工作的ES - 此活动的EF)

示例题

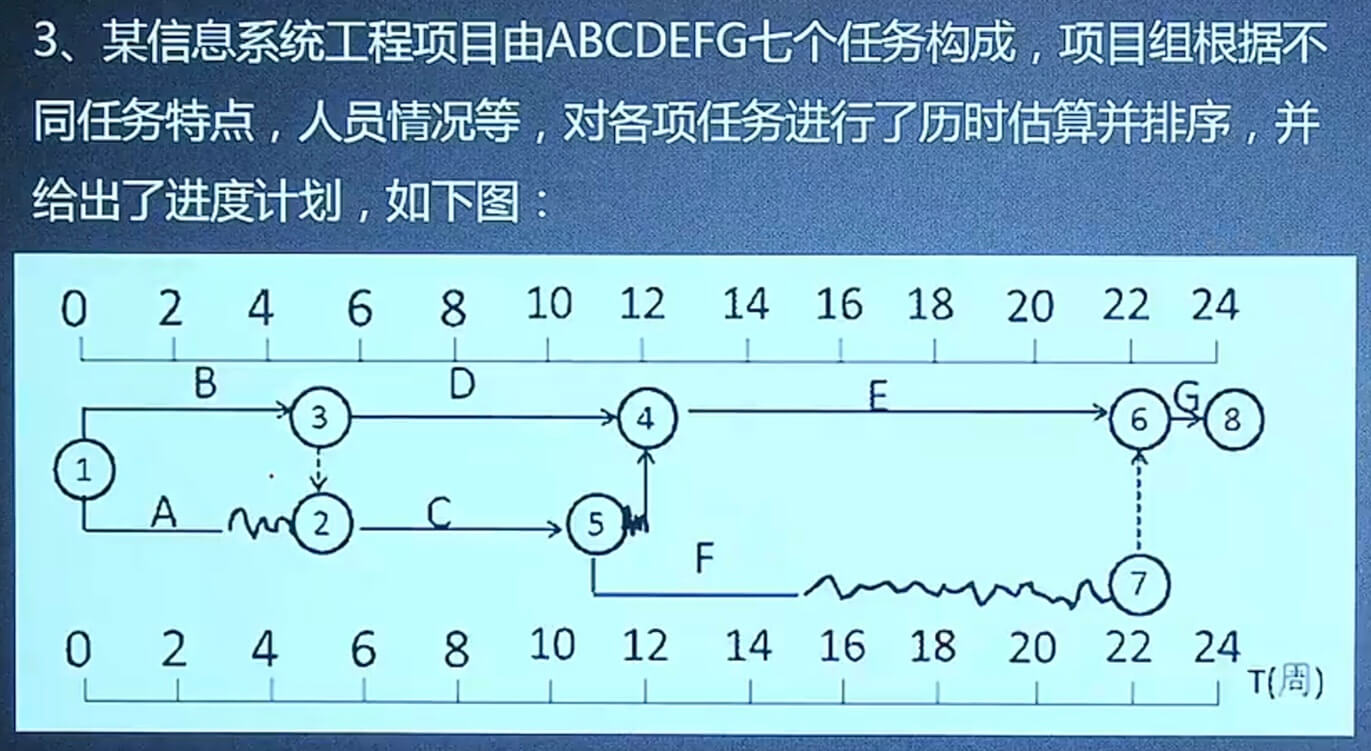
指出该项目的关键路径、工期？
本例给出的进度计划图叫什么图？还有哪几种图可以表示进度计划？
请计算任务A、D和F的总时差和自由时差？
若任务C拖延一周，对项目的进度有无影响？为什么？

答：

关键路径为BDEG，工期为24周。（不带波浪线的路径为关键路径）
时标图或双代号时标网络图。单代号网络图、横道图、甘特图。
A的总时差为3，自由时差是2；D总时差为0，自由时差0；F总时差为7，自由时差为7。（以x为起始点到终点G的波浪线的长度为总时差；以x为起始点到紧后工作的波浪线长度为自由时差）
对进度无影响。因为：对项目的进度有无影响即，对总工期有无影响（求总时差），C到工作结束的波浪线长度为1，所以总时差为1，拖延一周不影响总工期。

六标时

总浮动时间(总时差) = LF - EF = LS - ES

自由浮动时间(自由时差) = min(紧后活动的ES) - EF

ES	DU	EF
	ID
LS		LF

三点估算

三点估算中常用的两种概率分布：三角分布和贝塔分布

期望值: 通过计算得到，最期望的值 T1
悲观值: 题目给出，最糟糕情况 T2
乐观值: 题目给出，最好的情况 T3
最可能值: 题目给出，一般的情况 T4 不同的地方，符号可能不一样。

标准差 = (悲观 - 乐观) / 6 或 (大 - 小) /6 必须为正值

三角分布

适用于初步估算、数据不足或风险分布未知时，需要快速估算且对精准度要求不高。期望值：T1 = (T2 + T3 + T4) / 3

贝塔分布（PERT）

能更精确的反应最可能值。期望值：T1 = (T2 + T3 + 4 * T4) / 6

项目经济评价

静态投资回收期法

P = (累计净现金流量开始出现正值或零的年份 - 1) + (上年累计净现金流量的绝对值 / 当年净现金流量)

示例题

题目： 某IT公司计划投资开发一个项目管理系统，初始投资为100万元。预计该系统投入使用后，每年可为公司节省运营成本并带来收益如下：

年份	第1年	第2年	第3年	第4年	第5年
净现金流量(万元)	20	30	35	40	45

请计算该项目的静态投资回收期。

解答：

步骤1： 列出各年累计净现金流量表

年份	净现金流量(万元)	累计净现金流量(万元)
第0年	-100	-100
第1年	20	-80
第2年	30	-50
第3年	35	-15
第4年	40	25
第5年	45	70

步骤2： 找到累计净现金流量开始出现正值的年份从表中可以看出，第4年累计净现金流量首次出现正值(25万元)。

步骤3： 应用静态投资回收期公式 P = (累计净现金流量开始出现正值或零的年份 - 1) + (上年累计净现金流量的绝对值 / 当年净现金流量)

P = (4 - 1) + (|-15| / 40)

P = 3 + (15 / 40)

P = 3 + 0.375

P = 3.375年

答案： 该项目管理系统的静态投资回收期为3.375年，即3年4.5个月。

解释： 这意味着公司需要3年4.5个月的时间才能通过该项目管理系统产生的净现金流量收回初始投资的100万元。在项目决策中，如果公司设定的投资回收期标准是4年以内，那么这个项目是可以接受的。

运输问题

把某种产品从若干个产地调运到若干个销地（多对多），求运输费用最低的方案

伏格尔法

算出各行列中最小元素和次小无素的差额
对行差和列差进行对比，找出最大差额。以与最大差额值同行（或同列）的最小运价为准，倾其所在行的产量，最大限度地满足所在列的需求：一旦需求（或库存）被彻底满足（或库存调光）则随即划去该列（或行）的所有运价信息。（注意产量和销量的变化）
对未划去的行列重复以上步骤，直到得到一个初始解。

示例题

题目： 某软件公司有3个开发中心（A、B、C），需要向2个客户地点（甲、乙）交付软件产品。各开发中心的产能、各客户的需求量以及运输成本如下表所示，求最低运输成本的分配方案。

运输成本表：

	甲地	乙地	产能
A中心	3	1	7
B中心	4	5	9
C中心	6	2	18
需求	5	29	34

解答过程：

第一轮计算：

计算行差和列差：
- A行：次小值3 - 最小值1 = 2
- B行：次小值5 - 最小值4 = 1
- C行：次小值6 - 最小值2 = 4
- 甲列：次小值4 - 最小值3 = 1
- 乙列：次小值2 - 最小值1 = 1
找最大差额： C行差额4最大
分配： C行最小运价是2（C→乙），C中心产能18，乙地需求29
- 分配：C→乙 = 18（C中心产能用完）
- 更新需求：乙地剩余需求 = 29-18 = 11
- 划去C行

第二轮计算：

剩余表格：

	甲地	乙地	产能
A中心	3	1	7
B中心	4	5	9
需求	5	11	16

计算行差和列差：
- A行：3 - 1 = 2
- B行：5 - 4 = 1
- 甲列：4 - 3 = 1
- 乙列：5 - 1 = 4
找最大差额： 乙列差额4最大
分配： 乙列最小运价是1（A→乙），A中心产能7，乙地需求11
- 分配：A→乙 = 7（A中心产能用完）
- 更新需求：乙地剩余需求 = 11-7 = 4
- 划去A行

第三轮计算：

剩余表格：

	甲地	乙地	产能
B中心	4	5	9
需求	5	4	9

只剩B中心，直接分配：

B→甲 = 5
B→乙 = 4

最终分配方案：

A中心 → 乙地：7单位
B中心 → 甲地：5单位
B中心 → 乙地：4单位
C中心 → 乙地：18单位

总运输成本： 7×1 + 5×4 + 4×5 + 18×2 = 7 + 20 + 20 + 36 = 83

验证： 产能总计：7+9+18=34，需求总计：5+29=34 ✓

指派问题

有n项任务，恰好有n个人可以分别完成其中任何一项，应指派哪个人完成哪项任务（一对一），才能使效率最高

匈牙利法

首先找出每行的最小值，然后该行每个数值都减去这个数，得到一个矩阵。
在上面的矩阵中，再找出每列的最小值，然后该列每个数值都减去这个数，又可以得到一个矩阵。
在第2步所得的矩阵中，0即为可以安排的对应工作。

示例题

题目： 某软件公司有3名程序员（A、B、C）和3个开发任务（甲、乙、丙），每个程序员完成各项任务所需的时间（小时）如下表所示。请用匈牙利法求出使总完成时间最短的分配方案。

效率矩阵（完成时间）：

	甲任务	乙任务	丙任务
A程序员	9	2	7
B程序员	6	4	3
C程序员	5	8	1

解答过程：

步骤1：行变换（每行减去该行最小值）

A行最小值：2，减去2后：[7, 0, 5]
B行最小值：3，减去3后：[3, 1, 0]
C行最小值：1，减去1后：[4, 7, 0]

得到矩阵1：

	甲任务	乙任务	丙任务
A程序员	7	0	5
B程序员	3	1	0
C程序员	4	7	0

步骤2：列变换（每列减去该列最小值）

甲列最小值：3，减去3后：[4, 0, 1]
乙列最小值：0，减去0后：[0, 1, 7]
丙列最小值：0，减去0后：[5, 0, 0]

得到最终矩阵：

	甲任务	乙任务	丙任务
A程序员	4	0	5
B程序员	0	1	0
C程序员	1	7	0

步骤3：寻找最优分配 从矩阵中的0元素寻找分配方案：

A程序员 → 乙任务（矩阵中A行乙列为0）
B程序员 → 甲任务（矩阵中B行甲列为0）
C程序员 → 丙任务（矩阵中C行丙列为0）

最终分配方案：

A程序员完成乙任务：2小时
B程序员完成甲任务：6小时
C程序员完成丙任务：1小时

总完成时间： 2 + 6 + 1 = 9小时

验证： 这是所有可能分配方案中总时间最短的方案。

博弈论

找出A中各行的最小值
找出对A中各列的最大值
同时被1和2选中的元素即为对策的最优值，对应的策略分别为局中人的最优纯策略

示例题

题目： 两家互联网公司A和B在考虑产品定价策略。公司A可以选择高价或低价策略，公司B也可以选择高价或低价策略。下表显示了在不同策略组合下公司A的收益（单位：万元）。请用博弈论方法找出公司A的最优策略。

收益矩阵（公司A的收益）：

	B选择高价	B选择低价
A选择高价	8	2
A选择低价	6	4

解答过程：

步骤1：找出A中各行的最小值

A选择高价行：min(8, 2) = 2
A选择低价行：min(6, 4) = 4

各行最小值中的最大值：max(2, 4) = 4

步骤2：找出A中各列的最大值

B选择高价列：max(8, 6) = 8
B选择低价列：max(2, 4) = 4

各列最大值中的最小值：min(8, 4) = 4

步骤3：寻找鞍点 同时被步骤1和步骤2选中的元素：4

位置：A选择低价，B选择低价
行最小值 = 列最大值 = 4，存在鞍点

最优策略：

公司A的最优策略：选择低价
公司B的最优策略：选择低价
博弈的均衡收益：4万元

解释： 在这个博弈中，无论对方选择什么策略，公司A选择低价策略都能保证至少获得4万元的收益，这是A公司的最优纯策略。同样，B公司选择低价也是其最优策略，因为这样可以最小化A公司的收益。

一些不太好记的概念和公式 ​

挣值分析 ​

EV、AC、PV、ETC、EAC、VAC等概念 ​

计算公式 ​

AI生成的帮助理解图表 ​

总时差、自由时差 ​

六标时 ​

三点估算 ​

三角分布 ​

贝塔分布（PERT） ​

项目经济评价 ​

静态投资回收期法 ​

运输问题 ​

伏格尔法 ​

指派问题 ​

匈牙利法 ​

博弈论 ​

一些不太好记的概念和公式

挣值分析

EV、AC、PV、ETC、EAC、VAC等概念

计算公式

AI生成的帮助理解图表

总时差、自由时差

六标时

三点估算

三角分布

贝塔分布（PERT）

项目经济评价

静态投资回收期法

运输问题

伏格尔法

指派问题

匈牙利法

博弈论